|
关于几何非线性有限元计算
1、工程应用场合
5 j1 }' X: o8 Z4 A+ ^% ^$ A几何非线性主要应用计算如下情况:
& W% A4 G5 Z; u4 A-单体部件(梁和壳体)发生较大的变形;! H! O2 A, ]* b" y$ v7 ^" J) V q
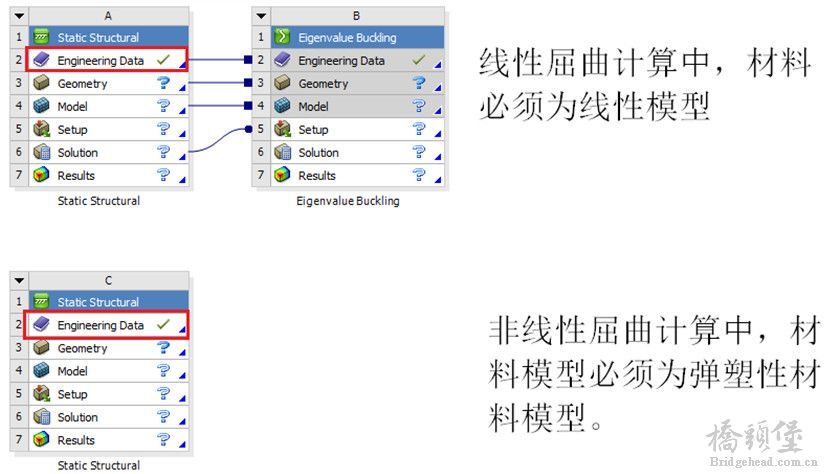
-非线性屈曲计算;/ K6 R! h3 R- r' O
-塑性成形计算; y4 Y0 ?& B% h6 U
-瞬态动力学的计算) k- V& C8 B8 Q' G
-含有橡胶部件的计算等
2 J6 `- t! B" W$ N
2 O1 V _! h* E* U7 f. _+ C
1 X. D; G) b! v& a4 B
 $ C9 \+ t$ |3 ~; z2 t+ w* J
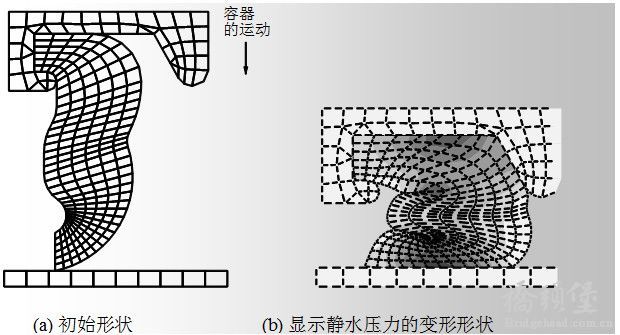
$ H% t0 A9 K8 T: T7 e这是一个大应变分析的例子,一个轴对称的橡胶密封件受压缩。分析包括接触,当密封件折叠时会发生自身接触。1 {; S9 Y. h/ i6 \% a1 ]9 v
( I& |+ }$ _# |! q+ o
- d+ s( n; V& ?
$ C9 \+ t$ |3 ~; z2 t+ w* J
$ H% t0 A9 K8 T: T7 e这是一个大应变分析的例子,一个轴对称的橡胶密封件受压缩。分析包括接触,当密封件折叠时会发生自身接触。1 {; S9 Y. h/ i6 \% a1 ]9 v
( I& |+ }$ _# |! q+ o
- d+ s( n; V& ?
 4 p: @0 Z, O/ h8 `+ B- |+ z' _9 _. T* l' S+ J8 o
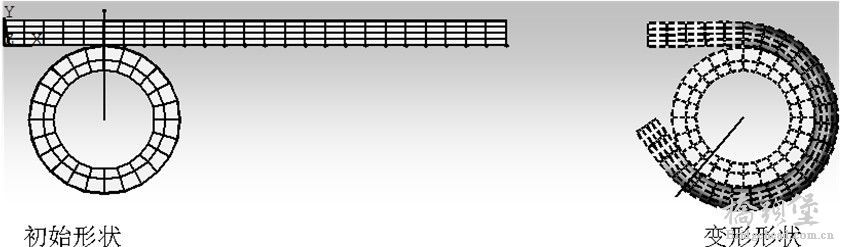
此例显示了绕轴线捆扎一根钢条。将金属弯曲成不同的形状是生产中常见的操作。在此例中,应变达到25%,顶端旋转接近270 度; S; _: [/ T6 V" [' [, p
1 D- ]8 a5 q/ \5 N1 @" m+ O2、计算原理
, x& L$ C4 C8 G" S, \' I1 B: _几何非线性的本质是把结构的变形对结构的刚度考虑到总体刚度矩阵中。
" a5 p- J. q/ d' n1 J' m& q4 f- K9 Z) ^; j. |9 V- y, B
4 p: @0 Z, O/ h8 `+ B- |+ z' _9 _. T* l' S+ J8 o
此例显示了绕轴线捆扎一根钢条。将金属弯曲成不同的形状是生产中常见的操作。在此例中,应变达到25%,顶端旋转接近270 度; S; _: [/ T6 V" [' [, p
1 D- ]8 a5 q/ \5 N1 @" m+ O2、计算原理
, x& L$ C4 C8 G" S, \' I1 B: _几何非线性的本质是把结构的变形对结构的刚度考虑到总体刚度矩阵中。
" a5 p- J. q/ d' n1 J' m& q4 f- K9 Z) ^; j. |9 V- y, B
 * h+ \* \8 t1 u- O' ^2 B$ Y
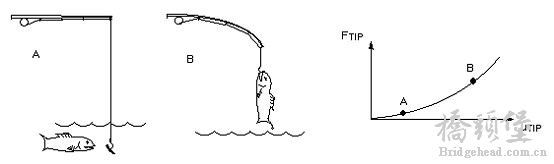
& i* B2 @8 B" P; J对于几何非线性问题包括以下问题: P5 Q3 ^7 c+ o& t& p6 [1 M
-大变形,大应变;; x0 m& P# ~- e# r7 l: u+ S
-大变形,小应变;9 q# H8 P: {0 M! w z
-旋转软化;
, R. V$ ~8 b U @2 Q" J0 K-应力刚化等9 x, ^% v8 P: g4 z
目前在ANSYS Workbench平台中,只需要在分析系统中的分析设置中进行激活即可。7 h4 N3 |5 m$ T
如果一个单元的形状发生改变(面积、厚度等),它本身的单元矩阵会发生改变。+ V2 a1 f. l6 C8 ?7 b3 ]
* M3 d" Q% n' [: {' `
* h+ \* \8 t1 u- O' ^2 B$ Y
& i* B2 @8 B" P; J对于几何非线性问题包括以下问题: P5 Q3 ^7 c+ o& t& p6 [1 M
-大变形,大应变;; x0 m& P# ~- e# r7 l: u+ S
-大变形,小应变;9 q# H8 P: {0 M! w z
-旋转软化;
, R. V$ ~8 b U @2 Q" J0 K-应力刚化等9 x, ^% v8 P: g4 z
目前在ANSYS Workbench平台中,只需要在分析系统中的分析设置中进行激活即可。7 h4 N3 |5 m$ T
如果一个单元的形状发生改变(面积、厚度等),它本身的单元矩阵会发生改变。+ V2 a1 f. l6 C8 ?7 b3 ]
* M3 d" Q% n' [: {' `
 * \4 b( D: N, z5 ?5 d# h8 I P: A/ j" g! |
0 u4 E4 s2 w7 w如果一个单元的取向改变,它的单元刚度向整体刚度的转换矩阵将发生变化。
: D/ R, k9 E4 f0 e9 i
" ?7 u8 p: q9 s) c) \) t/ U) Q& x: Z( g
* \4 b( D: N, z5 ?5 d# h8 I P: A/ j" g! |
0 u4 E4 s2 w7 w如果一个单元的取向改变,它的单元刚度向整体刚度的转换矩阵将发生变化。
: D/ R, k9 E4 f0 e9 i
" ?7 u8 p: q9 s) c) \) t/ U) Q& x: Z( g
 * I2 a6 l# Q. B" _; D
5 z8 T7 v0 d- z _* n6 g5 D如果单元应变产生了明显的面内应力 (膜应力),垂直于面的刚度会明显受影响。. C# u3 [3 d2 E4 y+ f& R# I
. ~9 }. N1 d$ y# }( E- V I8 D
R I z7 e! Y4 O+ y
* I2 a6 l# Q. B" _; D
5 z8 T7 v0 d- z _* n6 g5 D如果单元应变产生了明显的面内应力 (膜应力),垂直于面的刚度会明显受影响。. C# u3 [3 d2 E4 y+ f& R# I
. ~9 }. N1 d$ y# }( E- V I8 D
R I z7 e! Y4 O+ y
 ( m/ z+ n; @3 b0 f c# z9 ~9 k3 Z
( U3 q. k0 x# s/ m i* ^, S: K" A& P" G6 B. c
( X) `0 D, h0 j! C4 s1 m
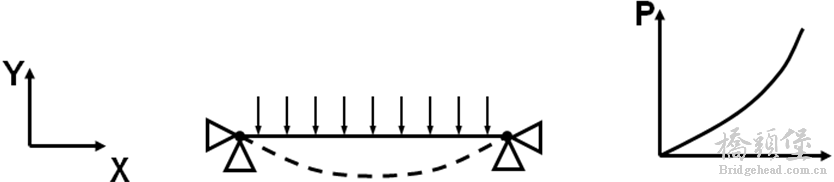
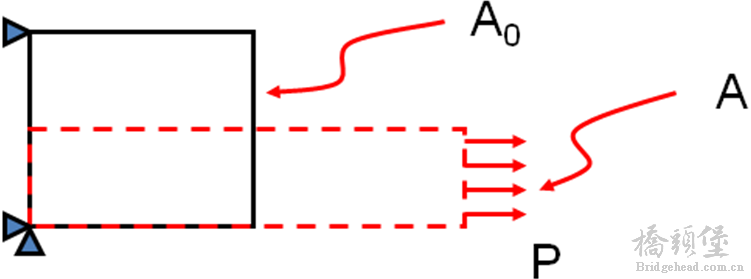
随着垂直位移的增加 (Y),大的膜应力(SX)导致刚化响应。
4 E5 `$ W9 Q- d2 s% j# i将非线性应变定义推广到一般的三维情况
- E, y2 [: N# G: u; d" E& o在二维和三维中, 当一个元件经历大应变变形时, 不仅长度元素改变, 厚度、面积和体积也改变
- ~$ P4 ]& X @/ Y) o% d' P% r5 j' {
( m/ z+ n; @3 b0 f c# z9 ~9 k3 Z
( U3 q. k0 x# s/ m i* ^, S: K" A& P" G6 B. c
( X) `0 D, h0 j! C4 s1 m
随着垂直位移的增加 (Y),大的膜应力(SX)导致刚化响应。
4 E5 `$ W9 Q- d2 s% j# i将非线性应变定义推广到一般的三维情况
- E, y2 [: N# G: u; d" E& o在二维和三维中, 当一个元件经历大应变变形时, 不仅长度元素改变, 厚度、面积和体积也改变
- ~$ P4 ]& X @/ Y) o% d' P% r5 j' {
 2 b) E1 {. }- @+ e( p' X1 ^" H, e# x5 T
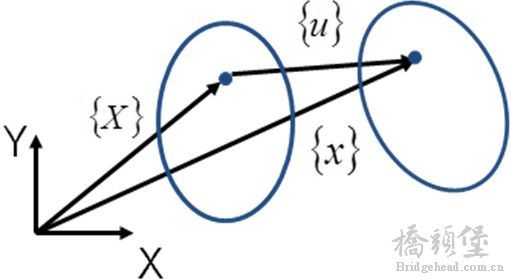
运动和变形
% u+ H$ t0 l) A7 w4 G
5 k8 p) b% M3 s, E物体在外载荷的作用下会移动和变形
4 @ \ V% r! Y( Q* i
& d! e, I- [& Q! Y
2 b) E1 {. }- @+ e( p' X1 ^" H, e# x5 T
运动和变形
% u+ H$ t0 l) A7 w4 G
5 k8 p) b% M3 s, E物体在外载荷的作用下会移动和变形
4 @ \ V% r! Y( Q* i
& d! e, I- [& Q! Y
 / o. t) o3 I" z- U$ q- ?6 R% U) d" q' \; [* {: w( \' @
如果考察该物体上某一点的运动, 它的初始位置为 {X }, 最终位置为 {x }, 则位移量为 {u }, 图中
# y6 |) g$ c ?/ ^ j: Y0 Q8 m8 I2 _7 `% z0 X0 N0 r0 Z
/ o. t) o3 I" z- U$ q- ?6 R% U) d" q' \; [* {: w( \' @
如果考察该物体上某一点的运动, 它的初始位置为 {X }, 最终位置为 {x }, 则位移量为 {u }, 图中
# y6 |) g$ c ?/ ^ j: Y0 Q8 m8 I2 _7 `% z0 X0 N0 r0 Z
 ! y# j/ P8 c" S( c( f0 u! r
4 y5 G5 r/ E2 {变形梯度
# k; F- c, g) t' \! n; p变形梯度是物体变形程度的度量, 定义为7 {$ ~) f; w- g% k- ?8 K
5 d! F& c2 U& P6 S! W
! y# j/ P8 c" S( c( f0 u! r
4 y5 G5 r/ E2 {变形梯度
# k; F- c, g) t' \! n; p变形梯度是物体变形程度的度量, 定义为7 {$ ~) f; w- g% k- ?8 K
5 d! F& c2 U& P6 S! W
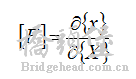 : ^# l5 u g$ {6 L- k: P2 H/ v; U
3 G1 {( O2 l7 Y" c5 v
变形梯度 [F ] 包含如下信息:
- q1 z6 T6 |2 C- q- Z! B体积改变: `- E5 M0 _* b# j& B7 w
转动
+ t" v; L; d6 z1 Z, z由于应变而引起的形状改变; s$ F }$ p+ Z5 u
• 大应变分析设定应变不再是无限小的,而是有限的或相当大的。
6 v, p- ]( C( H ]4 u8 M• 当应变超过一定百分比及不能忽视几何形状的改变时,可认为1 p$ Q; e" R8 k. i3 ~/ N9 @5 K1 F
是大应变。
9 a6 N4 z4 Z& } S: n0 p5 e& s• 大应变理论考虑了形状的改变(例如厚度,面积等等)及任何大旋转。
( @& G7 @2 S* g. l• 当单元旋转“ 大”到明显影响求解精度时,需激活大挠度效应。
+ c9 C/ l: E; c; y3 G* k7 k• 遗憾的是,没有明确的规定“ 大”到底有多大。“ 小”与“ 大”之间根据问题的不同相差非常大。
* f, m* |9 P( N, P% `
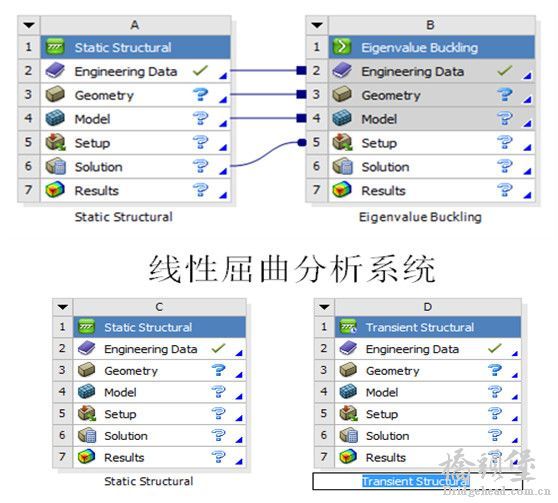
+ z; r& i6 F% D8 n& A6 n3、软件基本设置9 G5 W$ x9 J& @9 y& T3 N! U
. R; K! n, A4 g8 h' P; h
: ^# l5 u g$ {6 L- k: P2 H/ v; U
3 G1 {( O2 l7 Y" c5 v
变形梯度 [F ] 包含如下信息:
- q1 z6 T6 |2 C- q- Z! B体积改变: `- E5 M0 _* b# j& B7 w
转动
+ t" v; L; d6 z1 Z, z由于应变而引起的形状改变; s$ F }$ p+ Z5 u
• 大应变分析设定应变不再是无限小的,而是有限的或相当大的。
6 v, p- ]( C( H ]4 u8 M• 当应变超过一定百分比及不能忽视几何形状的改变时,可认为1 p$ Q; e" R8 k. i3 ~/ N9 @5 K1 F
是大应变。
9 a6 N4 z4 Z& } S: n0 p5 e& s• 大应变理论考虑了形状的改变(例如厚度,面积等等)及任何大旋转。
( @& G7 @2 S* g. l• 当单元旋转“ 大”到明显影响求解精度时,需激活大挠度效应。
+ c9 C/ l: E; c; y3 G* k7 k• 遗憾的是,没有明确的规定“ 大”到底有多大。“ 小”与“ 大”之间根据问题的不同相差非常大。
* f, m* |9 P( N, P% `
+ z; r& i6 F% D8 n& A6 n3、软件基本设置9 G5 W$ x9 J& @9 y& T3 N! U
. R; K! n, A4 g8 h' P; h
 5 Q, P/ N6 I( e5 q6 v6 C
* m" g# N# z; S$ h" M% x: J8 H1 ]$ @; w$ K9 n+ J& U6 X9 ^
& X, x: d1 L" j" N/ m" {4 V
5 Q, P/ N6 I( e5 q6 v6 C
* m" g# N# z; S$ h" M% x: J8 H1 ]$ @; w$ K9 n+ J& U6 X9 ^
& X, x: d1 L" j" N/ m" {4 V
 , E, N" B# I5 p4 {; X8 r+ u* |4 O3 P: H( @8 d; d2 Z
其他类型的大变形问题,根据实际情况,进行选择合理的材料模型。
5 }/ o5 T/ j" Y6 r4 V( u5 u
, S0 n. N J; K# W, s" @" q7 s2 }& b4 F
, E, N" B# I5 p4 {; X8 r+ u* |4 O3 P: H( @8 d; d2 Z
其他类型的大变形问题,根据实际情况,进行选择合理的材料模型。
5 }/ o5 T/ j" Y6 r4 V( u5 u
, S0 n. N J; K# W, s" @" q7 s2 }& b4 F
 9 Z8 A7 {, u* W' k0 ]! a ]; Z, g
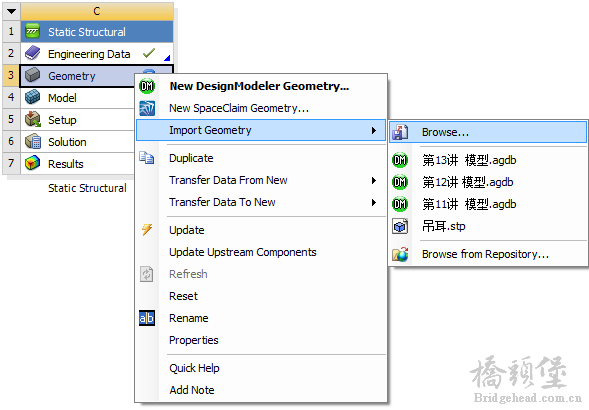
+ L J# e; ~+ j+ h6 R! D$ l对于几何模型,没有特殊要求,用户可以自己在DM中建模也可以从其他CAD软件中导入。
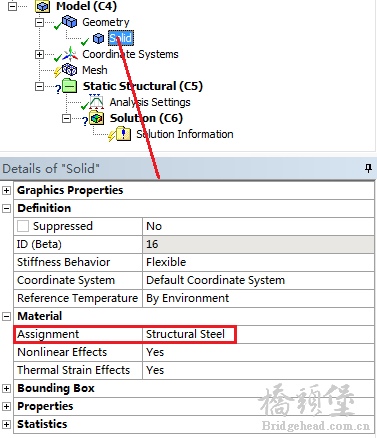
O1 H3 H5 n! f/ u将定义的材料模型,分配给对于的几何模型。
$ n/ x5 w% X$ x$ V; ^( ^: X5 }5 z/ t
9 Z8 A7 {, u* W' k0 ]! a ]; Z, g
+ L J# e; ~+ j+ h6 R! D$ l对于几何模型,没有特殊要求,用户可以自己在DM中建模也可以从其他CAD软件中导入。
O1 H3 H5 n! f/ u将定义的材料模型,分配给对于的几何模型。
$ n/ x5 w% X$ x$ V; ^( ^: X5 }5 z/ t
 5 K/ N+ e* B; F
6 b5 R# d7 V5 p- [* F# w3 n9 O& O
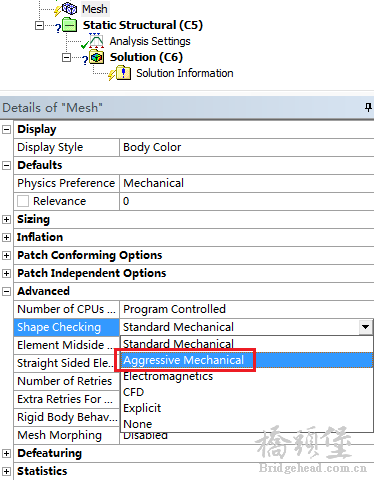
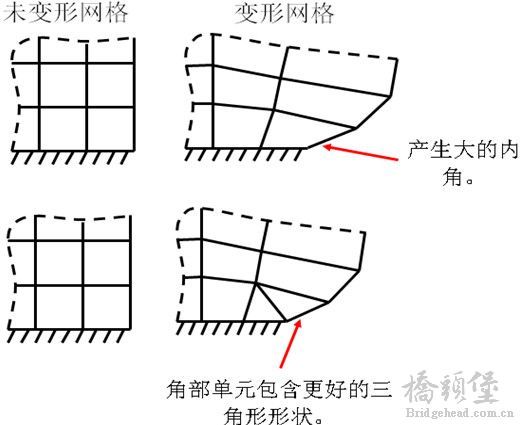
对于几何非线性问题,在Mesh中的高级选项中,将形状检查选项设置为Aggressive Mechanical- l. O$ U! R3 M! ~5 q
在建立大应变、大位移模型时避免使用带中间节点的单元。
, |$ t$ t: I% j/ n! S8 }带中间节点的(既高阶)单元在更新几何形状时,单元的中间节点可能穿过单元移动,导致产生负的旋转。8 w1 u; g/ R8 {, O' z4 ?4 o
6 d A6 i9 }/ u, Q5 A
5 K/ N+ e* B; F
6 b5 R# d7 V5 p- [* F# w3 n9 O& O
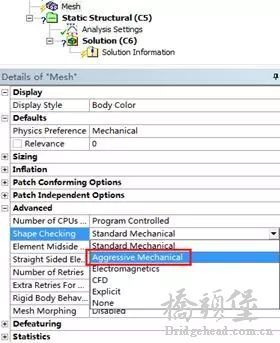
对于几何非线性问题,在Mesh中的高级选项中,将形状检查选项设置为Aggressive Mechanical- l. O$ U! R3 M! ~5 q
在建立大应变、大位移模型时避免使用带中间节点的单元。
, |$ t$ t: I% j/ n! S8 }带中间节点的(既高阶)单元在更新几何形状时,单元的中间节点可能穿过单元移动,导致产生负的旋转。8 w1 u; g/ R8 {, O' z4 ?4 o
6 d A6 i9 }/ u, Q5 A
 2 T/ \6 I2 \. E1 c8 W: ^6 ?
5 s% s3 p! ?" p. g) A5 H
# U" L( t# b% F# F1 P
2 T/ \6 I2 \. E1 c8 W: ^6 ?
5 s% s3 p! ?" p. g) A5 H
# U" L( t# b% F# F1 P
 ; E4 J- T$ Y) [+ X$ X) [( @
; _' L: @: k- K* Y
3 L4 A9 P4 Q1 F2 t4 Y/ v" P& i
; E4 J- T$ Y) [+ X$ X) [( @
; _' L: @: k- K* Y
3 L4 A9 P4 Q1 F2 t4 Y/ v" P& i
 * I7 \+ k H7 ^+ f$ Q. M
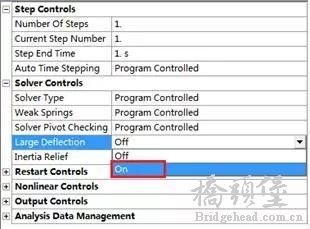
! _7 y G, F& o, Y在分析设置中,必须将Large Deflection选项设置为On,才能激活结构计算的大变形。' r$ W: V! X; Y' T: k0 ]
这个选项在存在橡胶模型的问题,必须打开,否则不能计算。
, J" o1 c8 a% g. Y/ S k7 u* x1 z0 K. y$ a
* I7 \+ k H7 ^+ f$ Q. M
! _7 y G, F& o, Y在分析设置中,必须将Large Deflection选项设置为On,才能激活结构计算的大变形。' r$ W: V! X; Y' T: k0 ]
这个选项在存在橡胶模型的问题,必须打开,否则不能计算。
, J" o1 c8 a% g. Y/ S k7 u* x1 z0 K. y$ a
 1 N2 Q) r' j6 t, `
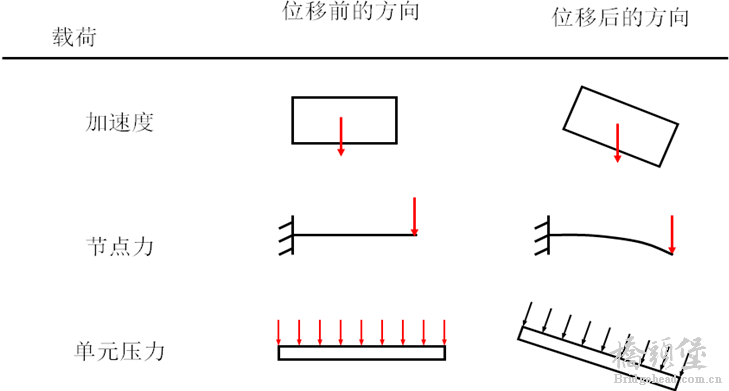
, J' ^7 w, L8 Q7 h9 }: U& z当结构经历大位移与旋转时,载荷发生了什么变化。 3 g1 N: Y$ e8 S d( p, h
在许多情况下,载荷将在变形过程中保持一致的方向。 . J1 G m, t1 j2 W
在另一些情况下,承受大旋转时,力将“ 跟随”单元改变方向。
2 g+ l. D$ U. a; ?* | M这两种情况ANSYS都可模拟,取决于施加载荷的类型。 ' g9 E. |7 T+ @7 f) k
加速度与集中力:
- i2 z+ d8 J5 b6 P保持它们的初始方向,忽略单元取向。
. I4 o( r1 @9 X/ w# Z& V表面压力载荷:1 z) M* h7 ?9 s! H
随单元旋转,因此总是垂直于变形单元的表面(这些是真正的追随力)。
) F: s2 |/ C* h7 D0 m1 m) _; D Z更新压力表面以计算大应变效应。因此,对于施加的常压力,总压力载荷将随表面积的改变而改变。
7 W( f" [2 Z M4 `
. x3 W3 ?5 B" u/ ~/ x- {" ?( V1 A& _$ l) W/ p3 t8 e
1 N2 Q) r' j6 t, `
, J' ^7 w, L8 Q7 h9 }: U& z当结构经历大位移与旋转时,载荷发生了什么变化。 3 g1 N: Y$ e8 S d( p, h
在许多情况下,载荷将在变形过程中保持一致的方向。 . J1 G m, t1 j2 W
在另一些情况下,承受大旋转时,力将“ 跟随”单元改变方向。
2 g+ l. D$ U. a; ?* | M这两种情况ANSYS都可模拟,取决于施加载荷的类型。 ' g9 E. |7 T+ @7 f) k
加速度与集中力:
- i2 z+ d8 J5 b6 P保持它们的初始方向,忽略单元取向。
. I4 o( r1 @9 X/ w# Z& V表面压力载荷:1 z) M* h7 ?9 s! H
随单元旋转,因此总是垂直于变形单元的表面(这些是真正的追随力)。
) F: s2 |/ C* h7 D0 m1 m) _; D Z更新压力表面以计算大应变效应。因此,对于施加的常压力,总压力载荷将随表面积的改变而改变。
7 W( f" [2 Z M4 `
. x3 W3 ?5 B" u/ ~/ x- {" ?( V1 A& _$ l) W/ p3 t8 e
 , b. h% @9 | P O
5 J2 g1 o S* p约束边界处的所有自有度,由于Poisson 效应将产出非常大的应变。
) N! P9 {6 M8 y4 d {$ z. k" m0 P& }2 X3 t, n
, G9 F1 G0 i7 N3 M- E3 k, t, a) x; v
, b. h% @9 | P O
5 J2 g1 o S* p约束边界处的所有自有度,由于Poisson 效应将产出非常大的应变。
) N! P9 {6 M8 y4 d {$ z. k" m0 P& }2 X3 t, n
, G9 F1 G0 i7 N3 M- E3 k, t, a) x; v
 4 `5 ^6 T/ T. A% H1 l7 }
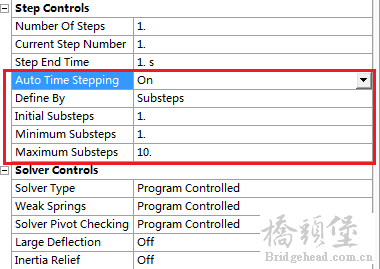
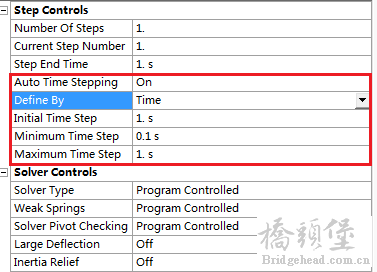
9 A! L8 T1 d( n& l在非线性计算中,子步(时间步)的设置非常关键,在静力学计算中时间没有实际意义,本质就是一个计数器和加载比例系数。 & o' ?3 I3 r* y( p$ T9 a1 b
: d \2 }7 F8 o( l+ J; V: l( _6 H# G8 o8 K: H$ h& |) k" [
4 `5 ^6 T/ T. A% H1 l7 }
9 A! L8 T1 d( n& l在非线性计算中,子步(时间步)的设置非常关键,在静力学计算中时间没有实际意义,本质就是一个计数器和加载比例系数。 & o' ?3 I3 r* y( p$ T9 a1 b
: d \2 }7 F8 o( l+ J; V: l( _6 H# G8 o8 K: H$ h& |) k" [
 " g; k% N9 F+ z/ N" @/ S+ v1 p3 H9 o% b
$ `5 S8 M, }3 b+ u8 p$ [4 U. J
" g; k% N9 F+ z/ N" @/ S+ v1 p3 H9 o% b
$ `5 S8 M, }3 b+ u8 p$ [4 U. J
 ! n* B. V: Q$ q6 Q L! W
+ \4 t' [2 O3 M% H7 U" F9 x" Y1 l
& N) o6 c6 A I' E E/ M7 L; D# l' P7 B" `9 R0 j. A0 v
- _ z! h' r; _$ p6 j; w# [7 g
! n* B. V: Q$ q6 Q L! W
+ \4 t' [2 O3 M% H7 U" F9 x" Y1 l
& N) o6 c6 A I' E E/ M7 L; D# l' P7 B" `9 R0 j. A0 v
- _ z! h' r; _$ p6 j; w# [7 g |
|