1. 斜拉桥设计计算特点
8 R$ }1 l6 } t9 U
斜拉桥是一种高次超静定结构(图1a),其自重引起的内力和变形可以通过调整斜拉索的张拉力而人为地进行调整。因此斜拉桥的设计计算策略与其它桥型有所不同。
# }4 A" l _; g
5 b/ M: y5 y/ t# V. C- k( T图1
在一般桥型如连续梁桥的设计中,一旦结构尺寸、材料和施工方法等确定下来,结构的恒载内力也就随之确定了,无法人为地再进行大的调整。而斜拉桥则不同,设计时是先通过成桥阶段的结构分析和调索,选定设计者所满意的恒载内力和变形状态(注意,关键是在一定范围内可选择,所以不同的人会选不同的状态),即所谓成桥阶段理想状态。然后以此状态为目标状态,寻找为达到该目标状态所需的施工过程和斜拉索的张拉力,即寻找所谓各施工阶段理想状态。两种设计计算过程简略示于图2中。
8 k9 d7 O" V7 W9 D7 z4 z
# @* ^/ E0 M7 n* C, h/ z4 Z
图2a 斜拉桥
, z7 I$ x$ `/ q: k3 ]( v" K
& z/ a8 X0 L! ^% c. ~图2b 连续梁桥
u2 a/ J ]+ p) G& Y9 q5 r' ~& q2.斜拉索的作用
% Y" C, \& n7 t/ A' m+ |
一般认为,对于弹性分析而言,斜拉索的作用是为主梁提供一系列弹性支承,如图1b所示。在荷载的作用下,主梁发生挠曲,使斜拉索伸长变形,因而产生拉力(相当于弹性支承的反力)。我们称之为“被动受力”,即其受力是因主梁的变形而引起的。这种比拟有一定的道理,但不确切。对于成桥后施加的荷载,如汽车荷载、二期恒载等而言,斜拉索确实相当于弹性支承。但对于主梁自重来说,就不完全是这样了。因为斜拉索在安装或调索时要进行张拉,这部分张拉力占斜拉索最终索力的大部分。而这种张拉力是以外荷载的形式作用在主梁和桥塔上的(图3),是一种“主动施力”,即它不是因结构变形而引起的拉力,而是其拉力引起结构的变形。正是由于斜拉索的这种主动施力的特征,才使得人们可以通过调索来达到调整结构内力和变形的目的。
7 X9 x9 G: l) [" _2 u因此可以这样说,对在斜拉索锚固之后由其他因素施加在主梁上的荷载而言,斜拉索对主梁起着弹性支承的作用。而对于在斜拉索锚固之前的结构而言,斜拉索是以其张力作为外荷载作用在梁和塔上来影响结构内力的。
- R9 I9 u( c7 U5 R" c# `& ^4 ?1 R$ i, t( a h8 G* z
# D% r% N4 o; \8 n
3.主梁受力特征
$ T5 t6 _+ u: r$ }
为说明问题,先分析一种特殊的情况,假设斜拉桥的梁和塔是一次性全部安装上去,并且斜拉索是同时张拉的,后面再分析实际分阶段施工的情况。
4 T4 K# z7 g9 z: Y" P5 K
根据前面的分析,主梁在其自重作用下的受力和约束状态不是支承于一系列弹性支承(斜拉索)上且跨度为斜拉索间距的连续梁,而是跨度为L1+L2+L1的连续梁或简支梁(视梁与塔墩的连接情况而定),其上作用着两个强大的力系,一个是梁的自重q,另一个是斜拉索的张力(图3)。这两个力系在梁中分别产生巨大的内力和变形,但因它们在竖向的作用效应方向相反且绝对值相近,所以梁的最终受力状态是两者之差。这个差相对于这两个力系单独产生的效应而言,其数值很小。而主梁的承载力也是按这个很小的差来设计的。
! e% M+ u& J+ D/ `
在两个强大力系作用下处于平衡状态的结构,其内力和位移对这两个力系是十分敏感的。只要其中任何一个发生了不大的变化,二者之差就会成倍甚至几十倍地变化。因此,与其它桥型相比,对斜拉桥的施工控制计算有更高的要求,因为施工中的误差可能会引起结构较大响应。
+ y8 w1 d% }+ I k5 a; w/ H7 I现举一简单例子来说明这种敏感性有多大。如图4所示,一跨度为L的简支梁,其自重荷载集度为q,在跨中作用一向上的集中力(相当于拉索的拉力)T=0.501qL。此时跨中截面的弯矩为
& }( i4 ^8 x! P1 U
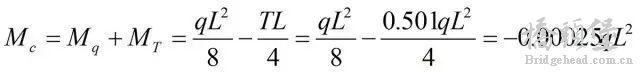 6 Z! o/ Y& _" X7 l
6 Z! o/ Y& _" X7 l现假定拉力T发生了+1%的偏差,则跨中截面弯矩变为
+ y# i8 A, c0 V/ [. p: B
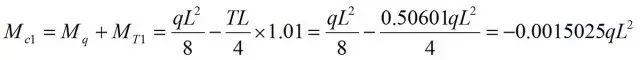 + t/ u& O4 Y. h" H* S
+ t/ u& O4 Y. h" H* S
变化量达
8 i+ g$ \) e# K6 j u, D1 C
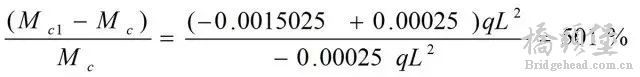 . H. w+ |% K# n0 |0 g
. H. w+ |% K# n0 |0 g上面讨论的是一种极端的情况,实际的斜拉桥是分阶段施工的,每浇筑或拼装一段梁就张拉一对索,直至合龙。这样,先安装的斜拉索对其后施加的荷载而言(包括其后的斜拉索张拉力和梁自重),就相当于弹性支承的作用,其拉力也因此而发生改变。因此,整个结构是由具有弹性支承且承受斜拉索张力和梁自重荷载的一系列结构逐步演变为成桥状态的。后面张拉的索和安装的梁段对前面已安装的索和梁段产生影响,但前面张拉的索和安装的梁段对后面安装的索和梁段则影响很小。
, z! E* Q0 h3 Q y9 r显然,对这样形成的结构,其内力和位移对前述两个力系的敏感性应该介于图1b和图3或图4所示情况之间。下面举一个实际结构的例子来说明其影响。图5所示为一座斜拉桥,跨度为194+518+194米(不计辅助墩的话),全飘浮体系,施工方法为悬臂拼装,计算时分阶段模拟实际的施工过程。成桥后中跨四分之一跨度处的恒载弯矩为-11669kN-m,由跨中向塔方向数第二根索处弯矩为最大弯矩(绝对值最大),其值为-13257kN-m。假如将斜拉索的初始张力减少5%,则中跨四分之一跨度处恒载弯矩变为最大弯矩,其值为-17193kN-m,增加了约47%,原最大弯矩处变为-13415kN-m,仅变化了约1%。之所以跨中附近变化量很小,是因为该处的梁段和索是较晚安装的,受其它索的影响很小。
: a- L* ?9 j; k; n5 p$ A1 \; B% ?0 |
z7 {5 V* C* |$ X4 j
/ t* V. l! i( U0 `4 n9 Y9 [图5
初学者容易产生的认识错误:“既然斜拉索拉力是一种荷载,那么对线弹性体系,因荷载与内力或位移成正比。所以,若斜拉索拉力变化,结构的内力也会成比例地变化。例如,若索力增大一倍,则内力和位移也随之增大一倍”。从上面的例子可以看出,结构的总内力并不与T(或q)成正比,而是与二者的综合作用成正比。事实上,线弹性体系的荷载与内力或位移之间的线性关系是指总的荷载与总的内力或位移之间的关系,而不是与力系中某一个或某几个力之间的关系。
- c1 F) T$ _, R& [3 L4.活载作用情况
0 N& r; e% ?& q
对活载来说,斜拉索相当于梁的弹性支承(图1b)。但由于其弹簧刚度较小,因此若活载较大,例如铁路荷载,就会产生较大的变形和内力。这就是相对而言,为什么斜拉桥在铁路上应用不如公路上普遍的原因。当然,这并不是说铁路桥梁不能采用斜拉桥形式,近年来我国铁路或者公铁两用斜拉桥已经取得了令人瞩目的成就。
7 s# ]6 S! N6 ~1 ]- s9 r
作者简介:
李乔,西南交通大学教授,博士生导师,茅以升桥梁研究所所长,在中国公路学会桥梁分会等学术组织任常务理事或理事,在土木工程学报等重要学术期刊任编委会委员或副主任委员。
$ B" `, }5 u& |+ u; W6 W+ b/ p) p本文转自微信公众号——西南交大桥梁之“李乔说桥”专栏+ y; ^ R. D( I# S: M7 y9 Q2 _& o
# v$ T( f7 V0 z. \3 P' u* f+ X1 y1 P+ _
4 y9 g) L: \+ R- N1 \. L5 Q) ]