建筑与结构的图形化共识 ——图解静力学引介

建筑与结构的图形化共识 ——图解静力学引介 01
; R9 g% h% j& Z7 s/ F2 Z+ Ya Graphical Consensus Integrating the Architecture and its Structure: a Brief Introduction of Graphic
% J) V% {, p* m" [! S

（因本文较长，图片较多，分为3部分）

* J: I& E: b: F" M  q& L前言

- v! w% O  s0 P% N       建筑的造型是所有建筑师都关注的终极目标，而那些有结构形式而致的建筑造型，往往是令建筑师们极为向往而又难以企及的：从安东尼•高迪（Antoni Gaudi，1852-1926）到皮埃尔▪路易吉▪奈尔维（Pier Luigi Nervi，1891-1979），从圣地亚哥▪卡拉特拉瓦（Santiago Calatrava 1951-）到伊东丰雄（Toyo Ito，1941-），我们可以看到，建筑设计的造型追求在结构的形态上取得直接的统一。然而这种统一，就必然要求对建筑学科与结构学科知识体系上的隔阂进行填补；尤其是建筑设计与结构设计在思维方式上存在的巨大“鸿沟”需要逾越。“图解静力学”，正是这样一种有助于两种传统的知识体系和思维方式之间沟通的桥梁。特此引介给中国的建筑师和结构工程师们，望有助于中国当代建筑创新进程中的深入探索。
# P# N0 ~) a  D' B5 I
创造性的前提之一：建筑师与结构师的技术共识
+ H  Z3 Z* c9 H       在这个全球性事物同质化严重的时代，无论发达国家的还是发展中国家的建筑业界，都努力在为巩固或寻找各自的建筑文化位置探索创新。支撑建筑实践的三大专业分别是：建筑、结构、设备（水暖电等）。而建筑与结构相互作用毫无疑问地在建筑设计创新中占据很重要的部分，其中阻碍建筑设计创造性的重要因素之一，就是建筑师与结构师的各执己见。于此矛盾，享誉国际的结构工程界大师林同炎 教授早在1988年就一针见血的指出：“在结构工程与建筑专业之间继续存在着技术共识的空白。而相应的教学和现代信息的分离又继续限制着建筑师与结构工程师之间创造性地相互配合的可能性。这种制约在设计项目的方案阶段尤为重要，致使建筑空间形式和技术思路之间整个关系不协调，从而增加以后的设计阶段出现较大矛盾的机会。”  
       而事实上，长久以来，“结构选型”为填补建筑师与结构师之间技术共识的空白作出了巨大努力。

当下盛行的技术共识：结构选型
5 _1 W* Z) j9 m' h+ D( h       得益于对“结构选型”的认知，建筑师懂得了怎样的建筑空间形式需要怎样的结构类型，而结构师知道了怎样的结构类型契合怎样的空间形式乃至风格。陈保胜教授将主要的结构形式分为：梁板结构、桁架结构、单层刚架结构、拱式结构、薄壁空间结构、网架结构、网壳结构、悬索结构、薄膜结构以及高层建筑结构，并论述各类型的优缺点，以供设计师合适地为空间形式选择结构类型，也为结构师考虑结构类型在空间的效用提供依据 。而“结构选型”作为国家一级注册建筑师考试科目——建筑结构的组成部分 ，就说明其重要价值及其盛行的原因。国外对结构分类的思路基本与国内是一致的，如由日本建筑构造技术者协会对结构类型的分类几乎完全与国内的分类方式相同 （图01）。英国著名工程师托尼•亨特（Tony Hunt） 对结构类型的分类更为抽象：实体式（solid），平面式（surface），骨架式（skeletal），模式（membrane）和混合式（hybrid） ——但这些类型与国内的结构选型却是相似的。
% y. _' d; J1 V5 L( E

01 4 g, Y! T9 Z9 N" W2 X$ n7 w+ M! {

0 B  Z9 w+ ]% C       林同炎教授和S.D.斯多台斯伯利（Sidney D. Stotesbury）教授“意欲在方案设计和初步设计阶段填补（建筑师与结构师之间的）这种空白”  而撰写的《结构概念和体系》，也涵盖了“结构选型”。虽然这本书强调的是“先进的设计思想可以通过概念设计充分地展现。一个结构项目工程师的主要任务就是在特定的建筑空间中用整体概念来设计结构的总体方案，并能有意识地利用总结构体系与各基本分体系之间的力学关系，而不仅仅是能精确地计算和分析一个给定的分体系或构件。”   但依据林老先生对结构的特殊分类（结构总体系、水平分体系，竖向分体系、直线型水平构件、直线型竖向构件…）此书同样可以被理解为作者在综合各种建筑设计与结构设计要素之后，以精妙的方式，有预谋（建筑设计和结构设计的互动关系）有层次（总体结构和分体系结构的主次关系）有顺序（整体设计到局部细部的设计流程）地论述如何将“结构选型”更有效地运用于设计。

0 M* G% t% v1 H' |2 p2 k结构选型容易被接受的原因：模型思维
$ ?/ v) c) u  N0 }0 e  j: w2 Z       “结构选型”能够被结构师接受，得益于其自身知识体系内就已包含如何操作科学模型（scientific model）。对这种根源于十八世纪晚期和十九世纪早期的法国理工院校  （国内结构知识体系多源于此体系）的传统结构工程师思维，汤姆▪福▪彼得斯（Tom F. Peters）教授将其定义为“模型思维”（model thought）。他指出“模型思维”作为设计师与建造师在实践活动中的一种思维模式，有别以经验(empirical)为主思维模式,是一种基于现代结构科学分析方法的思维模式：“将建筑分解为构件，从而简化结构师的计算和比较工作。由此，理论家们将结构分裂为简单、二维的模型，诸如梁、柱、拱以及次级像悬臂梁、连续梁、联结梁等结构类型。通过铰接或刚接的方式将这些模型链接起来的新事物，也被称为新结构模型。结构师分析和测量每个构件，然后将它们组合为更为复杂的形态或者次级形态，并最终形成整个结构。一言概之，他们将结构定义为有等级的系统组成，自下而上分别是构件、连接、组件、次系统，最后是整体。”这种同时他指出了这种思维方式的两个重要缺陷：1.缺乏对建筑结构三维性以及时间维度中（time dependent）结构效应（如材料疲劳）的思考；2.不能在理论和实际中及时反馈 。 在“结构选型”知识体系中，以代数计算（algebraic calculation）为主的结构师，能更方便地将具有不同数值特性的结构体系进行分类，从而建立起与建筑师图示化沟通的平台。
0 `4 C. j% ]* L% L$ Y. S       “结构选型”之所以易于被建筑师所接纳，甚至轻易超出他们对三大力学（理论力学、结构力学和材料力学）的认可，很重要的原因是这门知识符合建筑师以图形思考的方式。事实上，同样是在法国理工院校的知识体系内，建筑学教授路易斯▪迪朗（Jean-Nicolas- Louis Durand，1760-1834）在十九世纪早期为创立现代的建筑学知识体系时，就从结构的支撑类型与建筑空间形态的关系。在法国综合理工大学（the école Polytechnique）的档案馆（archives）里，保存着迪朗的一个学生A.弗朗索斯（A.Fransoz）自1823年来的笔记（图02），从中“我们依旧可以发现迪朗通过解释空间与结构的关系得出的不同建筑结构的类型。” 这显然是“模型思维”在建筑学的理解和延伸。
2 G5 Y, A$ `" e5 x) R

02

: v2 s$ U1 `; J, }
" h/ u3 v, E1 F       建筑学的知识体系中，“结构选型”不但为现代大型建筑项目建立建筑师与结构师的图形为基础的技术共识——如空间网架筑造出蓬皮杜艺术中心（Pompidou Centre，建筑设计：伦佐▪皮阿诺Renzo Piano 和理查德•罗杰斯 Richard Rogers，结构设计：奥韦▪阿鲁普公司Ove Arup & Partners，图03&04）宽阔自由的室内空间。
% |- M/ L, f/ G6 P% @  {

03 ( L6 H2 g3 L: D

* E' p2 a; f( P$ e. b

04

3 B2 u1 }4 x8 |  x6 D7 _$ G4 X
2 X. l. w2 h& s& j% @9 U       又如悬索结构创造了国立代代木体育馆（国立代々木竞技场，建筑设计：丹下健三Kenzo Tange，结构设计：川口卫Mamoru Kawaguchi，图05&06）结构与艺术统一的屋面。同时，“结构选型”也为普通的建筑项目提供技术依据。

05 $ }/ `6 N; W: Q$ c. n

06

3 d0 h$ D0 {. v9 X! X, q' j7 b+ k4 c       在普通的建筑项目实践中，建筑师在默认某种结构类型后，集中思考该结构类型下的不同空间形式可能。我们可以认为建筑师没有更多考虑其他的结构类型，但却不能否认建筑师选择了该结构类型——无论这种结构是经验的判断还是科学认知。例如勒•柯布西耶（Le Corbusier，1887-1965）在1914年提出的多米诺房屋（Maison Dom-ino）就是在选定这种“无梁楼板-柱支撑”结构类型的基础上，再着手对空间可能性的探索。“提契诺学派”（Ticino School）的建筑师们更是在实践中，将场地、材料、体验融入空间与结构关系，设计出触动人心的建筑，如马里奥▪博塔（Mario Botta）设计的卡登那佐住宅（Residence in Cadenazzo，图07&08）。因而“结构选型”为建筑师提供了图形思维下空间与结构关系的途径。
8 V' S  t' `! _+ x# z

07

08

1 S% K( I% \' i& g$ d
       作为建筑学基础教学的“空间加减法”，在一定程度上进一步弱化了“结构选型”中结构的代数特征，而强化了空间形式与结构类型之间的不同关系。在教学领域“德州骑警”（“Texas Ranger”） 的约翰▪海杜克（John Hejduk，1929-2000）对“九宫格”（nine-square problem）的探索将其发挥到极致。
       毫无疑问，“结构选型”这种“模型思维”为建筑设计的创新提供了保证。然而，在当今中国的现实中反复上演的一幕却是：
% _* t, j* g9 u7 x0 u: i建筑师：这个形式是我所需要的。
结构师：但我们做不出这种结构。
7 g; i. l& S, z: i$ J3 W建筑师：别人都做得出来，为什么你们做不出来？
4 }8 S  B+ e) i2 y2 V结构师：这是国外结构师做的，国内还达不到这个水平。
…
; h$ \4 u# i. T+ z0 c1 A. H       为此，我们有必要进一步深究“模型思维”究竟在什么范围内提供了抑或限制了创新。
3 |0 `* o* ?  b! d7 C
+ |' y7 Q- R$ r4 y) M. s“模型思维”的优势与局限
; J+ a/ z& \5 d3 Q       我们先思考“模型思维”在何种程度上为我们带来创造性。在大型建筑项目中，“模式思维”利用先进的技术可以在空间（如蓬皮杜艺术中心）和形式（如国立代代木体育馆）等方面为建筑提供了创造性。在普通建筑项目中，“模式思维”下的建筑师在选择适合的结构类型后，通过运用场地关系、材料质地、细部构造等非结构要素创造新的空间体验（如卡登那佐住宅）。因此确切的说，“模型思维”为建筑师与结构师的合作提供了既定的可图示的结构类型——遵循于结构工程专业提供的类型，建筑师可以进一步受益于先进技术或者场地材质，创新建筑。
" t, u) ?; _* z' M7 E& R0 ^       但是，如果当建筑师对空间形式的要求超出了给定的结构类型，显然“模型思维”无法再为建筑师与结构师提供交流的平台。那么，当建筑师与结构师之间出现矛盾时，各自期望向对方提出怎样的要求呢？
       通常，以概念草图、功能泡泡图、比例等图像进行思考设计的建筑师在创造形式时，并非依靠结构知识，而是源于概念或者视觉思维模式——而且他们渴望这条道路畅通无阻，并期望尽快得到结构师的反馈意见。而结构师期望建筑师在形式创新的伊始就拥有结构知识的支撑，以便他们能沟通、理解和深化——问题是，结构师期望建筑师自身拥有怎样的结构基础呢？结构师自身的设计过程是：首先对建筑形式简化为不同节点类型的杆件模式，再计算不同荷载在杆件的受力（轴力、剪力、弯矩、扭矩、挠度等）状况，验证实际的材料尺寸断面能否承受最大荷载情况。除了将形式简化为结构模型，根据计算绘制受力图，其余大量反复的代数计算与验算就是结构设计的操作——这已经打破了建筑师和结构师之间“结构选型”的只基于图形的技术共识。如果遵循这样的结构计算流程做建筑设计，一来没有结构师存在的必要，二来建筑师的创造效率变得极其低下。
       无疑，图形化-代数化（algebraic-graphic）的“模型思维”无法为非常规形式设计中的建筑师和结构师提供高效便捷的技术共识。这种情况下，既然代数思维方式是建筑师与结构师之间快速沟通的阻碍，若仍旧期望建筑师与结构师之间有效的合作，就需要寻找建筑师与结构师都能容易接纳的快速的可靠的图形思维方式。
: i5 a7 j' X! H1 t$ V* ?+ z/ v% E1 J2 e       那么，在传统的结构知识之内，是否存在为非常规结构形式提供图形化的技术支持？
+ {8 L8 W$ S( s
传统的结构知识之内：弯矩图法
! h$ W4 {9 h, q# k0 n* q, J       一些作者在解读建筑设计与结构之间的关系时，会研究结构承载的弯矩图与结构形式之间的关系。
; q9 T4 |1 V- `9 I( r       诺曼▪福斯特事务所（Norman Foster & Partners）与阿鲁普公司设计的雷诺中心（Renault Centre，位于英国Swidon，1980-1982，图09），作为高技派重要的建筑之一，其形式无疑是在结构选型提供的既定结构之外的。对于建筑形式和结构力学的关系，安格斯▪J▪麦克唐纳（Angus J. Macdonald）用结构的弯矩图，揭示了二者的一致性，他认为这个梁柱（post-and-beam）非常规形式（non-formative）的结构，其轮廓正符合由重力的均布荷载作用下弯矩图的形式（图10） 。

09

! }4 t! M8 [( X: J6 O0 e

10

       这种弯矩图法并非个例，戴维▪P▪比林顿（David P. Billington）教授在解释罗伯特▪马亚尔 （Robert Maillart，1872-1940）的建筑设计——契阿索屋架（Chiasso Shed, 位于瑞士Chiasso, 1924，图11）时，也用与雷诺中心一样的弯矩图以及对弯矩图进行变形操作解释了结构的形式与内力之间的关系 （图12）——其钢筋混凝土桁架屋顶突破了钢筋混凝土结构厚重的美学成见。
; _8 S$ v: {* g

11

12

. d1 W! a, j# u" K- C4 t1 f# c


8 m6 q7 P$ g" i% w- }& o

建筑与结构的图形化共识 ——图解静力学引介 02
a Graphical Consensus Integrating the Architecture and its Structure: a Brief Introduction of Graphic Statics
+ u. N' _0 h; m; `$ x  o. d
传统的结构知识之外：图解静力学
% J  |: f: \' W+ `0 h+ {       历史上，很多伟大的结构师兼建筑师或者设计建筑的结构师，有惊人的能力把握乃至控制结构内部应力的分布与传递。
       西班牙的高迪（图13），爱德瓦多•托罗哈 （Eduardo Torroja, 1899-1961，图14），卡拉特拉瓦（图15），意大利的奈尔维（图16）等都用与力流概念相关的方式作为设计工具。高迪通常研究悬挂的自受力模型形态，将其反转后作为建筑形式。基于对力的分布和聚合形态的理解，奈尔维以力的传递路径布置钢筋混凝土的承重梁。托罗哈常常将结构看作压力和拉力的网络状分布。凭借对人体一些具备表现张力的特殊平衡姿态力的理解，卡拉特拉瓦创造相似内力路径的建筑形态。这些集结构与建筑于一身的大师们虽然是空间形式结合结构体系创新的典范，但其对应力传递的掌控却基于自身深厚的结构功底和建筑审美，以及丰富的实践经验。对于绝大多数建筑师和结构师来说，似乎望尘莫及。
5 W% u2 M* J( K1 m

13 2 ^* ]& |& p, G6 V2 p. O

14 & R3 W$ O$ X6 U3 e! @

15

' {8 w* p& q; ?. j" [& r: ?

16

1 m8 Q9 q8 n' J6 I+ I; f
       然而并非没有可供参考的建筑师与结构师合作的优秀案例——仙台媒体中心（Sendai Mediatheque,位于日本仙台，2001）的设计过程就是经典范例：在设计竞赛中，建筑师伊东丰雄首先以水草意象的概念草图作为设计起点（图17），之后进一步与结构师佐佐木睦朗（Mutsuro Sasaki ）达成以竹子作为结构原型的共识，最终创造出21世纪新的建筑类型（图18）。
' X8 \) X; K6 _9 P8 l! o$ {- l) x

17

18 6 n, h+ q. D# A6 e0 x7 f

& j8 n7 ~& F5 x1 x$ L       仙台媒体中心的案例中，我们可以发现建筑师和结构师以图形化的结构受力作为交流的媒介，而其最核心的要素就是对力传递的认识——即选择在形式和传力方面与概念契合的竹子作为仙台媒体中心的参考对象。并且显而易见，图示化的力传递作为建筑师所易于理解的结构依据，基本可操作性。
0 b$ c! d5 P' p% C0 a% A+ ^' o       这样一种，以全图形化的思维方式为基础，根据结构内部应力传递进行设计的方法，显然与传统的“模型思维”不同，它在结构形态的认知方面拥有比结构选型更大的自由度。然而，是否存在一种客观可靠的科学知识支撑这种思维模式呢？
; @9 g+ E& b& u图解静力学（graphic statics，或者graphical statics）。
: ^! w9 [+ F, T- G  r       在总结和梳理前人在图解计算领域的成就，并将其系统的运用于工程分析，瑞士联邦苏黎世高工（ETH-Zurich）的工程学院教授卡尔•库曼（Karl Culmann，1821-1881） 分别于1864和1866年出版了两卷《图解静力学》 (Die Graphische Statik)。这标志着图解静力学正式成为一门学科。
国内最早引入图形静力学的学者应该是唐山交通大学 的吕谌先生，在1936年（民国二十五年）他将J.T.怀特（J.T.Wight）于1913年编写的Elementary Graphic Statics 翻译为中文并命名为《图解力学》 。稍显遗憾的是他并没有写序说明引入该科学的价值，甚至没有将当时怀特写的序言（preface）一并翻译。所幸北京大学工学院建筑工程系主任朱兆雪教授在其1939年（民国二十八年）编写了《图解力学》的前言中阐述了当时引入此门科学的意义——相对于当时的结构力学知识，图解静力学在计算上更快捷清晰，这也正是其在欧洲盛行的原因 。由此可见当时结构工程的专业人士对图解静力学的认识正是基于该方法的便捷和易于掌握。近些年，彼得斯教授在2001年发表于《A+D》杂志的“营造文化和技术思维”，向国内读者提及了图解静力学，但并未详细介绍 。
* h( Z" L- d6 f2 m& U本文将graphic statics翻译为“图解静力学”是因为这门学科只解决力学的两个分支之一“静力学”（statics），以区别与之相对的“动力学”（kinetics）。另外需要注意的，吕谌先生翻译的和朱兆雪教授编写的《图解力学》均是以结构分析为目的的，有别于本文以设计为导向的意图。关于这门知识，事实上，对国内建筑师和结构师来说，其中极小部分知识我们已经学过——力的分解与组合的平行四边形法则，以及共点力的平衡（图19）。只是我们把这小部分知识作为现行结构知识的次级知识使用——用其简化荷载以方便代数计算。
9 w6 X7 Z" k& |- d' V+ f2 `

19

. }0 h. H& M" d
) F3 R8 e3 K& F; S' g* M       图形静力学最基本的方式是基于互补（reciprocal ）关系的两个图示：形图解（form diagram）和力图解（force diagram） 。其中形图解是平衡状态下结构的形及其力（荷载）在其上的位置，而力图解是外力（外部荷载）与结构内力的矢量平衡关系。两个图解之间是相互决定的，即互补（reciprocal）。 另外需要指出：在同一种外力分布情况下，与之互补的力图解并非只有一个，而这通常是设计师融合形式与力流的选择策略。形图解和力图解之间的互补操作本文以悬索多短线（funicular polygon）结构为例介绍（图20）。
; G/ [3 _) F3 R( N# U

20 $ F% p- ~0 q$ l

0 d) P) I) `/ J+ y
* s+ v' |, c5 Q$ x! S( L       其中a为形图解， b为力图解，图中外部矢量力（包括方向direction和量度magnitude）用f表示，以绿色实线绘制，并编号；而内部力用l表示，以黑色虚线绘制，其在力图解中以矢量力（包括方向direction和量度magnitude）的形式出现，但在形图解中只保持方向性，并不再维持量度。图b力图解中汇聚一点并不断叠加的闭合三角矢量回路（closed force polygon），就是图a中受力各点并维持平衡的图解（原理同图19b）。例如图a中f1、l1和l2汇聚为一点并维持平衡状态，反映在图b中就是f1、l1和l2组成的闭合三角回路。图20是悬链线（catenary）的力学模型基础，如果将整个模型上下颠倒过来，就是拱受力的力流路径——通常被称为推力线（thrust line）。这两种连续多段线或者曲线 的力流模式，是图解静力学中相对简单的类型。 而图解静力学常常被进一步用在桁架（truss）的力学分析中 ——如屋架或桥梁，乃至混凝土或者膜结构的设计。
      
弯矩图法与图解静力学对比研究
( L8 g" e& _9 Y  R4 f% M8 {        面对非常规建筑形式，虽然在结构选型的设计方法之外，我们至少还有弯矩图法和图解静力学两种方式可供选择，但对于进行实践的建筑师来说，哪种方法在什么地方对建筑设计具有建设性意见，便极具价值。因此有必要二者进行对比研究。
+ O/ |  A! p* \# _  S) X1 g. b" m       关于弯矩图和图解静力学之间的关系，爱德华•阿伦（Edward Allen）和瓦克罗•扎莱夫斯基(Waclaw Zalewski)在麻省理工学院 (MIT)关于图解静力学简单网页操作（Active Statics online） 的内容中年就暗示了弯矩图和图解静力学之间的关系（图21）。

21 . _( J; v0 j8 [4 O  h- K

# T# L9 q" m( n  I. }
       明确提出弯矩图和图解静力学相似关系的是约瑟夫•席沃扎（Joseph Schwartz）教授，他在苏黎世高工一年级结构设计教学的课本 中揭示了弯矩图和图解静力学的形图解具有非常一致的关系（图22）。这种启示对结构认知来说是巨大的进步，然而作为建筑设计，有必要理解图形中（无论弯矩图还是形图解）线条的由来及对设计的意义。
3 z& Z* j6 N+ }5 f8 b" V& A

22

% [% X- j% c; }       本文仍旧以雷诺中心为例，对两种方法进行比较和辨识。
0 C1 E" ^2 j; s" t' t       首先我们将结构的边界与荷载情况定义如图23——竖向均布荷载，端部悬挑的对称结构，与地铰接。

23

4 g6 }9 E7 Q0 L5 c4 d) l       此种情况下，弯矩图的画法，至少有两种。第一种（图24）是借助常用弯矩图表，通过组合不同部分的弯矩 ，就可得到本结构的弯矩图。然而这种弯矩图中最确切的是最大值的数据，而最大值之间的线性曲率如何却是模糊的——这与传统结构计算中只要求对弯矩（或组合弯矩）最大值进行安全限度的设计有关密切。
. g# d; H" e' h6 f" [" t( ~4 g5 x

24 & @/ p) h( ~% Y& t8 C1 B# a

4 D) z2 Y. n% ^( E8 Z+ ~9 _5 P( r/ S
2 v6 z7 G: n: m( a       第二种（图25）则是将均布荷载转化为均匀的集中荷载，通过分段代数计算结构平衡状态下各点弯矩值，再将各点连接绘制成更为精准的弯矩图。

25 - V3 d# E  I* T

       然而，从设计操作的角度，我们对弯矩图的图形意义提出三点疑问：
# m+ \2 d7 d% \) s       1.弯矩图中即使确定了各点值，但在绘制弯矩图时，这些数值可以按照一定比例绘制得出数值相同却线型坡度/曲率不同的多段线/曲线（图26），那么这对于形式的进一步确定有何指导意义？

26 1 E* A; _) \/ v* Y, ~. u/ G. D/ S8 K( y

. w& N4 n0 D2 r) q. ~
6 x! P- U. l) h6 A! S6 Z8 l# Z+ d       2.按照传统结构知识规定所绘制的弯矩图（图形绘制于材料受拉一侧）与麦克唐纳提供的弯矩图是倒置的关系（图27），这对建筑设计形式操作的意义，但我们有什么科学依据放心大胆的作出此判定？

27 ( y7 C: y/ S3 U

       3.弯矩图通常用阴影表示其面域（图28），对设计来讲，这些被线段囊括的部分究竟有何作用？

28 9 n* H8 G# i3 ^! l6 j9 q/ [: K9 }

       图解静力学的方法相对弯矩图更为直观——通过先求解支座反力，再根据图解静力学力图解和形图解的操作，就得出结果（图29）——与弯矩图法几乎一致的形，却为以上三个疑问提供了建筑设计建设意见的解答：

29 2 a# |9 s; ]/ M) h8 e# G$ o: H5 Y+ z

: i4 O! _6 P8 k8 A2 w& @
& D2 `. l; Y1 Y' Y3 A       1.在图解静力学中一定的线型（即形图解）对应了特定的内力值（即力图解），通过对形与力的关系的理解（图30），建筑师能更科学的选择材料（抗性、断面等）。

30

! `1 P2 }8 m) H7 {8 K
0 D* Z/ y0 Q- \  n2 [- [       2.图解静力学为线性的倒置关系提供了科学依据（图31），为此，我们可以理解高迪为何能运用倒置的模型进行建筑设计。

31

       3.图解静力学中形图解求解出的表示力传递路径的多段线已经是平衡状态，多段线围合的区域为建筑设计洞口的设计提供了可能（图32）。
# [- Q' w; j5 T8 o3 @' d

32

' X+ o/ v) G$ U2 s! v8 V
) }! X% R4 ?- h  [& M$ w       当然，必须指出的是，弯矩图法在其他很多意义上也能够对建筑造型设计给出行之有效的指导建议。
8 J6 S; E' ]9 h/ `9 T5 H      
图解静力学与结构选型关系的进一步思考
3 T8 U3 ?8 W" `' p- G       一方面，以上对图解静力学的讨论，很容易让读者形成一种解读：某种意义上图解静力学向传统结构知识体系宣战。另一方面，中国建筑实践领域所处的状况却是：大多数建筑师对结构选型都不能运用自如，甚至不能正确运用。因此，在结构选型都尚未灵活掌握的今日中国，我们是否有必要再花时间研究图解静力学？
; _# E5 T; `3 b7 `       为回答这个问题，我们可以先思考阿伦教授等人对图解静力学的组织方式（图21）：其中用图解静力学求解的结构形式涵盖了悬索、拱、几种桁架形式（简单支承或有悬挑）以及斜拉索结构，这些是二维的图形，所以无法包括三维的网架，另外涵盖的结构类型都是线性构件组成的，也就无从囊括实体结构(monolithic )的折板、薄壳或者轻质结构（light-weight）的膜或帐篷等类型。但这并不是宣告图解静力学只是对线型构件结构提供技术支持。
9 s7 b" T5 `$ d/ x       奥利里奥•穆托尼（Aurelio Muttoni）教授在2004年进一步梳理和归纳了图解静力学与现有结构类型的关系（图33） 。从这张知识组织图中我们可以了解到，穆托尼不仅突破图解静力学在杆件体系应用的局限：涉及到混凝土等实体结构，也突破了图解静力学在二维平面的束缚：延伸到三维空间体系。同样，席沃扎教授在苏黎世高工的教学也采用与穆托尼类似的知识组织体系，拓展了图解静力学的实用范围 。
      

33

$ Y9 W8 p' j# W; g7 d       因此，我们可以看出，事实上在知识组织的形式上，图解静力学与传统的结构选型可以保持惊人的相似。而结合本文之前对图解静力学的诸多讨论，在设计初期，图解静力学除了能为非常规形式提供技术支持，也完全可以作为建筑师对结构选型知识深化理解和灵活运用的坚实根基。
8 S6 z8 Y3 C- Q; y5 ?1 V3 C

        建筑与结构的图形化共识 ——图解静力学引介 03a Graphical Consensus Integrating the Architecture and its Structure: a Brief Introduction of Graphic Statics

; `" J' ]" i7 @9 t
& G5 ^/ O8 ]% V9 f2 a“力流思维”及“力流”概念的梳理与澄清
       与由代数方程公式计算决定结构形态的“模型思维”不同，支撑图解静力学进行设计实践的思维方式与前文所提及的结构大师们的思维模式又是相似的——这是种掌控结构内部应力传递的思维，本文暂且称之为“力流思维”（Force-Flow Thought）。
       一提到“力流”，大家似乎都能很快对其有所领悟，但有又无法完全确信。 “力流”的英文为“force flow”。事实上，“力流”概念尚未成为正式的专业术语。英文的“force flow”无论在通用英语词典（如the Merriam-Webster online Dictionary 或者Cambridge Dictionaries Online ），或者专业的英语词典（如Dictionary of civil engineering , Dictionary of building and civil engineering ,或者McGraw-Hill Dictionary of Engineering ），甚至在介绍结构理论发展史的《结构理论史：从拱的分析道计算力学》（The History of the theory of structures: from arch analysis to computational mechanics ）一书中，均无收录。同样，中文的“力流”在通用的《现代汉语词典》 或者专业辞典《中国土木建筑百科辞典：建筑结构》 和《中国土木建筑百科辞典：工程力学》 都无记载。因此，“力流”仍旧属于非正式用语。因此有必要对“力流”这一概念进行梳理和澄清，以便我们更好的把握和运用。
       鉴于对“力流”界定并非清晰，而从模糊的理解来看，对“力流”的采纳是工程师为更好的理解和控制应力在结构实体内的传递。因此本文在梳理此概念时，将与之相关的内容也纳入思考，为下一步的澄清打下基础。总得来说，大致有三类：1.对“力流”有所定义或解释；2.无定义却使用“力流”概念；3.既无定义也未使用“力流”概念，但却使用类似的思维进行设计或理论工作。
/ i. R7 r# Q3 e# \2 Z8 X2 H* _       1. 对“力流”有所定义或解释。
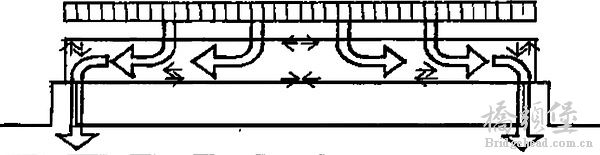
" S$ R5 r/ I% L' Q       对概念“flow of force”给出明确定义的应该是海诺•恩格尔（Heino Engel），他将荷载在实体（solids）内三个操作——“1.荷载接受（load reception）； 2.荷载传递（load transfer）；3.荷载释放（load discharge）”的过程称为“flow of force”（译本翻译为“力量的流动”并简称“力流”） ，并且用图示的方式呈现了均布荷载作用下，力在简支梁实体内的传递（图34）。此外，在2009年，Edward Allen和Waclaw Zalewski在著作中以一段对话的形式，将力在结构实体内的传递与水在河流中的流动类比，由此解释力流（flow of forces） 。需要注意的是，虽然二者都使用“flow of force”的概念，但我们需要进一步观察其是否一致。
6 h7 P) _0 s2 Z8 @

34 ; ^( _. R; ?/ u% d8 U

( r8 |5 m& X  }3 V  I' i# P1 O
; I+ f. N$ ]4 j3 W       2. 无定义却使用“力流”概念。
       一些书籍虽然使用“force flow”或“flow of force”对建筑结构的传力进行解释，但并没有给出明确定义。1977年，沃夫冈•舒莱尔（Wolfgang Schueller）用 “force flow”解释了结构构件尺寸和应力大小的关系（“The member sizes respond to the magnitude of force flow” ），并且暗示了“force flow”（力流）和“stress distribution”（应力分布）的关系 。法国著名的工程师米歇尔•维勒迪（Michel Virlogeux）则是将“flow of forces”应用于设计的倡导者，作为国际混凝土联盟（Fédération internationale du béton，即fib）的主席，他认为：“工程师在设计和分析结构时，必须知道力流（flow of forces），并对能够解决问题的结构和物理现象有清晰的理解” 。而在“结构形式的几何（Geometry of Structural Form,2010）”一文中，罗伦茨•拉乔尔（Lorenz Lachauer）和托尼•科特尼克（Toni Kotnik）则直接使用了“force flow”：“基于图解静力学的技术，借助几何图解（geometric diagrams）在建筑结构内的力分布已可视化。这种对力流的图解呈现允许对建筑形式的结构形态进行绘制（description）。” 我们对此同样需要谨慎各学者对“force flow”的理解是否一致。
       3.既无定义也未使用“力流”概念，但却使用类似的思维进行设计或理论工作。
       这一部分涉及更宽泛的使用范围，不仅包括诸多理论家也同样有很多实践家。
诸如高迪、托罗哈、奈尔维、卡拉特拉瓦等工程师兼建筑师也都没有明确使用过“force flow”这一语汇，却已此种思维模式进行思考实践。
       高迪在设计中使用的是“力多边形”（polygon of forces） 的概念。根据圣地亚哥•胡亚塔（Santiago Huerta）教授对高迪的研究，在奎尔公园的挡土墙与廊柱（the porticos and retaining walls at Parque Güell）的设计中，高迪在设计图纸中将力多边形直接叠加于设计的建筑形状之上（图35），得到力与形的统一 。

35 3 n* G5 r( ~% ^! A. p- R

9 ?6 \- \# S1 t$ b: ]) h       托罗哈在设计中使用的是“主应力”（principal stresses）和“应力分布”（stress distribution）结合的概念。他将实物中主要应力的分布看作网络（grid）或者由铰连接的桁架（struts interconnected with hinges）的图形 ——同样是叠加于设计图形之上，利用具有方向和粗细的线条（lines of certain direction and thickness）直观的表达了应力的传递和密度（the transmission and intensity of stresses），比如它们如何在特定区域聚集，又如何传递与消散的 （图36）。

36

' B% N' N  j, X
$ x. [3 G8 k: w- k3 n       奈尔维则更偏向于使用“主弯矩等应力线”（the isostatic lines of the principal moments）作为设计工具。他在波伦亚国家烟草专卖局(the state tobacco monopoly in Bologna)大型仓库的楼板设计中便采用了此方法，“混凝土可塑性质的自由度，也即是建筑上的自由度，是如此的完整，以致肋的设计完全取决于结构需要，同时又得到相当的艺术效果。这种效果之一列，即如楼板体系所示，板肋是随着主弯矩的等应力线布置的。”
卡拉特拉瓦也没有明确采用“force flow”的概念，但很多学者对其建筑作品及理念的介绍和研究都传达出该概念在其设计中的重要作用。拉菲尔•L•布拉斯（Rafeal L. Bras）教授将卡拉特拉瓦的建筑看作是力的流动（flow with the forces）或者包含矢量力的结构（the force vectors seem to merge with the structures）与建筑形态的融合 。
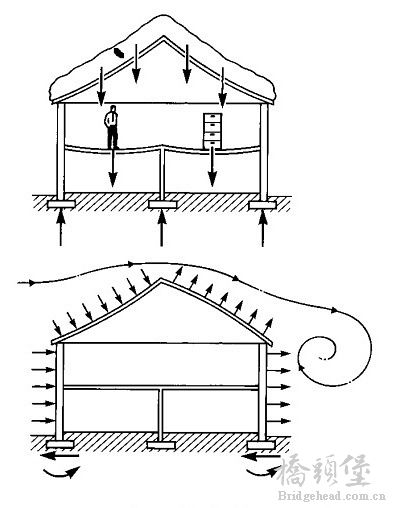
      用图形化的方式表达力在实体中的传递，对理解结构在建筑中的效用是直观高效的，这也是为什么很多学者在解释原理和理论时常用的此种方式。麦克唐纳曾用图示的方式表达了不同荷载在房屋结构内的传递（图37）——“作用在房屋表面的荷载，其中由雪荷载和房间里的物件导致屋面和楼板结构弯曲，并致使墙内形成压力。风导致房屋外表面遭受压力和拉力（suction loads）” 。
  R' ^; i2 z: Y

37 4 c, }/ \0 K" X3 X

5 ], {6 b& c& P5 N; x( R
       以上这三种分类对应力和形态的关系有着各自的理解，但共同的特征是：用空间分布的应力，将其并置于实体图形，表达力的传递——这就是“力流”概念的基础。然而这种界定并不确切。这又引出另一个问题：是否概念够用就不许需要确切的理解？
! |. J2 _$ s* K# g) @, K5 T为此，需要对“力流”的概念做进一步澄清。
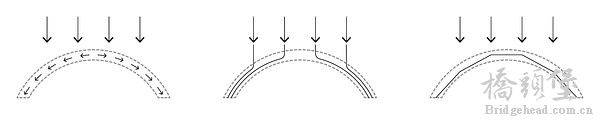
       以拱为例，有至少三种方式用叠加于结构实体中的空间分布应力表达力的传递（图38）。

38

$ U9 g; z5 f% w" j6 J; p2 Y
+ G- m5 z% S6 i8 Q/ D/ ]+ Y  H- F       这三种方式的在图形上的区别：a用箭头的，非连续的方式表达了力的传递；b用连续的线条（曲线或多段线）表达了每个力的传递；c则用多段线的方式表达了力的传递及其整体的关联——一种整体静力平衡关系。a相对于b，不能更准确地直观力的传递路径；而b相对于c，不能确切表达力传递时的整体关系。事实上，c的绘制是基于图解静力学的（图39）。也正因为此，a和b都无法在图形中提供相关的内力数值以供参考，而c则直观在提供准确的力的传递路径时也提供了相应内力值。

39

8 i7 p" F1 \9 x" d       而三种方式的澄清，对于建筑学的意义分别在于：a为理解建筑和结构的模糊关系提供了示意性的表达，但基于其非连续的特征，甚至无法为所学者提供力在传递过程中出现节点的位置，而且这种方式不能为设计实践提供科学基础；b为理解建筑形体和结构力学的大致关系提供了思路，虽然相比于a，能为所学者提供可能节点的信息，但和a一样，这种方式仍属于对已有实物的可能荷载的解读，同时无法提供内力值信息，因此不能作为设计操作所需的科学知识；c则以图解静力学为基础，既能提供准确的形与力的关系，以供建筑设计形式确定的需要，又能借助图解静力学的力图解提供内力的数值，为建筑设计材料的选择提供参考。
       由此可以看出，对不同方式使用范围的区分有助于我们在合适的时候选择合适的方式。
基于以上讨论，我们能够非常清楚，图解静力学提供的第三种传递表示，对建筑实践（无论是建筑师单独思考形式还是与结构师进行交流）是最科学的。因此本文将“通过将空间分布并各部分均静力平衡的连续力系，叠加于结构实体图形上的，对结构形式进行研究的思维方式”，定义为“力流思维”。

; G* m+ N* g, X7 k“力流思维”的运用
: S  l% O! E! r# U+ l! A* E7 m       细心的读者会很快意识到“力流思维”就是图解静力学中形图解与结构形式的叠加——但这并非笔者所期望的。因为的确形图解与结构形式的叠加是科学准确的方式，但伴随着设计者对图解静力学运用的累积，有足够的可能凭借丰富的经验在概念设计阶段多出模糊但具备可行性的判定，而缩短设计概念思考的周期。
7 }6 ~8 T' W3 r( }8 D       仍旧以拱作为“力流思维”运用的例子。
       首先借助图解静力学中对均布荷载下力拱形传递路径的认识，我们可以将其叠加于两种有裂缝的实拱（顶端上部裂缝或顶端下部裂缝），通过避开裂缝位置控制力的传递路径，由此理解有裂缝的实拱为何可以继续保持稳定（图40）。这是概念层面上建立的力与形式的关系，并非需要通过形图解与力图解建立精确的关系。

40 ) k, }9 `& Q4 c( u( {# T( y) B

! S1 W6 t) F, k+ k
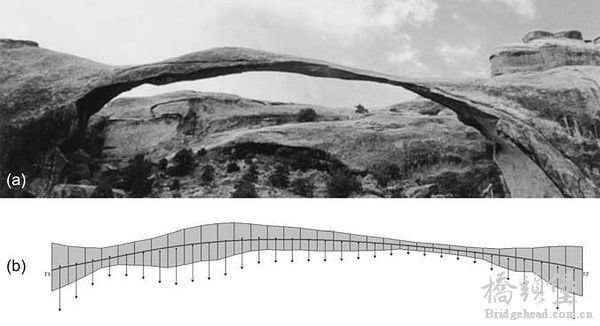
       在进一步的应用中，可以再采用较为精确的图解，如菲利普•布洛克（Philippe Block）教授利用此概念对自然界奇异现象用图解静力学的方法进行分析（图41） ，用力的合理传递路径解释了为何美国犹他州恶魔花园（Devils Garden， Arches National Park in Utah, USA）里这块天然纤细的石拱经久不毁。对同样的结构概念进行精确的图解操作，高迪用图解出的拱形力流线，用于设计奎尔公园的挡土墙与廊柱（图35）——这是就是被人们所迷恋的神秘高迪的创造力来源之一。

41

5 ~: Y) J; O* J1 D: l, v: Z) x

1 o4 A/ Z; P+ N+ y! d7 e; L       因此，基于设计师不可避免的同时积累科学与经验，有必要对“力流思维”保持开放的界定——即包括以科学为基础的精确图解计算，也包括以经验为依据的概念把握。
        
结论
       当下的中国建筑界，即作为世界上建筑量最大的一片热土，也作为对世界建筑形式的超级试验场。在这样的建筑造型竞赛中，中国建筑师的工作大部分处于一种模仿的阶段。我们坚信，只有通过建造和结构的知识与能力的充分掌握，才能真正突破这种模仿而进入造型原创的阶段。图解静力学，显然是一种相对容易被建筑师和结构式共同掌握的科学方法，并为两者之间的合作提供图形化的技术共识。它不仅以力流思维，为结构选型的模型思维模式提供了深化认知与操作的科学基础；也为非常规的建筑与结构造型探索提供了依据。为此，我们可以相信，图解静力学将为中国建筑与结构学界，在真正意义上的建筑形式创新提供一种有益的新手段。

" m7 Z/ _9 [3 N（在此感谢Tom F. Peters教授，和导师赵辰教授与Joseph Schwartz教授的指导，以及Joseph Schwartz教授工作室团队的帮助。感谢好友侯博文的校稿。）

* b/ B+ u3 y) L7 \  |: A图片来源：
01.日本建筑构造技术者协会 编, 《图说建筑结构》，周学军 等译，中国建筑工业出版社，2000。p.125.
9 ^9 E* o! \: R: M% O02. Ulrich Pfammatter. The Making of the Modern Architecture and Engineer. Basel: Birkhäuser, 2000. p.59.
, S# Y% \1 ~6 m' t$ x  X# O2 d( [03. [日]渡边邦夫 等著，《钢结构设计与施工》，周耀坤 等译，中国建筑工业出版社，2000。p.8.
8 D4 K* k( Z  H+ b, I% q* _04. http://farm1.static.flickr.com/166/419739442_9027ba8713.jpg
05. Malcolm Millais, Building Structures: From Concepts to Design (second edition). Taylor & Francis, 2005. p.313.
8 _9 O7 Q& t- ~06. http://www.scutde.net/t13courses/1307-njhhvbgkys/4/tu4/4-3-3-1.jpg
& O2 l% G$ Y7 `, n07. 冯金龙，张雷，丁沃沃编著，《欧洲现代建筑解析：形式的逻辑》，江苏科学技术出版社，1998。p.12.
08. http://bonifaciy-zen.livejournal.com/
09. http://www.fosterandpartners.com/Projects/0295/Default.aspx
10.笔者根据麦克唐纳Structure & Architecture 第70页插图绘制.
' J. n- [5 k1 \. c' H11. http://archivdatenbank-online.ethz.ch/
12. David P. Billington. Robert Maillart's bridges: the art of engineering. Princeton University Press, 1979. p.67
13. Bill Addis. Building: 3000 years of design engineering and construction. Phaidon, 2007. p.556.
14. Bill Addis. Building: 3000 years of design engineering and construction. Phaidon, 2007. p.583.
15. Alexander Tzonis. Santiago Calatrava: Complete Works. Rizzoli International Publications, 2004. p.172.
. }$ V( L( Y1 A1 X) C: `16. http://1.bp.blogspot.com/
) ]- ^% E% g- X2 D8 K9 B5 |& O9 g17. Toyo Ito. Blurring Architecture. Charta, 2000.02.
' L4 ?4 }, o3 Q18. Toyo Ito, Mutsuro Sasaki. GA Detail 2: Sendai Mediatheque. ADA Edita. 2001.04
$ j, [9 t& K4 [( X8 O  [) o21. http://acg.media.mit.edu/people/simong/statics/Start.html
8 L* i6 b$ ]  n, J* @2 ?1 ^22. Joseph Schwartz, Tragwerksentwurf  I (ETH Zürich 一年级建筑学结构设计课本), 2009. p.93.
5 }0 E8 L' r  \, S33. Aurelio Muttoni, L’art des structures: une introduction au fonctionnement des structures en architecture. EPFL Express, 2004 目录页。
34. [德]海诺 恩格尔 著， 林昌明 等译，《结构体系与建筑造型》。天津大学出版社，2003. p.7.
35. Santiago Huerta, “Structural Design in the Work of Gaudi”, in Architectural Science Review, vol. 49.4（2006）, University of Sydney, p. 328.
36. Eduardo Torroja Miret. Philosophy of Structures. University of California Press, 1958. p.12。
$ J" u6 W) b- ?( [37. Angus J. Macdonald, Structure & Architecture (second edition). Architectural Press, 2003. p.1, Fig.1.1.
40. Joseph Schwartz, Tragwerksentwurf  I (ETH Zürich 一年级建筑学结构设计课本), 2009. p.61.
% {8 |9 ^3 u  M$ h0 H8 Z$ M) K41. Philippe Block, Equilibrium Systems: Studies in Masonry Structure, Master dissertation in MIT, 2003. p. 18.
% C  m0 H" p1 a, ?- A
8 `+ B: _- L, x/ \7 P6 }% A7 p

把建筑的轮廓和moment diagram统一起来有什么好处吗?

        
        
1 Q& h4 n! V# y9 n弯矩图的形与建筑轮廓的形统一时，
1.更加经济，通常因此节省材料；
2.从某些理论视角，更加贴近建筑本质，远离附加之物。
$ N4 p" q3 `9 D1 E6 n% q9 v3 U在《form and forces：design efficient，expressive structures》一书关于梁的章节有介绍，结构外形与弯矩图轮廓一致时，构件只受轴力，没有剪力；材料轴向受力时的利用效率最高，因此这以为着可以节省材料。
/ V" _8 j0 g4 P! l5 x2 i