本帖最后由 西风独自凉 于 2011-3-22 14:26 编辑
合理成桥状态的确定原则
斜拉桥为高次超静定结构,任何一个构件状态的改变必然会引起整个结构受力状态的调整。斜拉桥的高次超静定及组合体系结构决定了其受力的复杂性,在设计中必须综合考虑梁、塔、索(及辅助墩),所以在确定理想成桥状态过程中,控制目标的选择必须主要考虑以下几个方面:
1)主塔 主塔是斜拉桥的最终传力结构,通常内力较大,塔作为压弯构件要求塔内弯矩不能太大,否则后期混凝土收缩、徐变的内力重分布会对塔极其不利(尤其对非对称斜拉桥而言),同时考虑到活载因素,在活载作用下塔向江侧的弯曲程度比岸侧大,并且混凝土后期收缩徐变的影响往往使塔往江侧偏,因而应保证主塔在恒载作用下,向岸侧有一定的预偏。 2)主梁
主梁是斜拉桥中直接承受荷载的结构,斜拉索索力较小的变化,就会使得主梁内力发生较大的变化。如何使主梁弯矩在恒、活载作用下弯曲应力小且分布均匀成为确定理想成桥状态的重心,所以主梁弯矩最小化是确定理想成桥状态 的主要控制目标。在成桥状态下,主梁的恒载弯矩要控制在“可行域”范围内。
3)斜拉索
斜拉索的索力从自身出发要满足两方面要求:斜拉索垂度要求的最小索力;材料强度要求的允许最大索力。索力要分布均匀,但又有较大的灵活性,通常短索截面尺寸小,索力小;长索截面尺寸大,索力大,从而保持全桥索力的分布均匀,但局部地方应允许索力有突变如0号索(当全为漂浮体系的桥型)和1号索的索力通常用较大的值:尾索由于起锚固作用,其索力通常取值较大,从而索的刚度较大,对活载受力有利。在所有的索中,不宜有太大或太小索力的索。
4)边墩和辅助墩
边墩和辅助墩支座反力在恒载下要有足够的压力储备,最好在活载作用下不出现负反力。但这种受力要求通常由配重或设置拉力支座来满足,值得注意的是,辅助墩反力大小主要受结构形式,跨径比例及中跨、边跨配重影响较大,而索力调整其变化较小。 确定合理恒载索力常用方法 结构优化设计就是从符合斜拉桥使用功能上的要求,同时满足强度、稳定性和刚度要求的所有可行设计中,相对设计者预定的标准,找出的最优化设计方案优化设计的数学本质是在约束条件下求极值的问题。一般是建立数学模型,将个工程结构的设计问题变为一个数学问题并结合合适的优化方法,通过计算机程序进行优化计算,得到优化后的结构设计。合理恒载索力确定方法有很多,根据给定的成桥目标,将已有的分析方法归结为三大类:指定受力状态法、优化法(无约束和有约束)及影响矩阵法。下面介绍本研究的方法: 最小弯曲能量法
弯曲能量最小法是以结构(塔、梁)弯曲应变能作为目标函数,从能量原理出发,设计合理的索力保证成桥后结构弯曲能量最小,来求出恒载下的合理成桥索力值。 有限元模型 索力对照表 索力编号
| 设计索力
| 主梁应变能最小时索力
| 主梁和塔应变能最小时索力
| 38
| 0.51636E+06
| 0.98414E+06
| 0.97578E+06
| 39
| 0.19435E+06
| 0.11272E+07
| 0.15469E+07
| 40
| 0.74558E+06
| 0.54880E+06
| 0.47220E+06
| 41
| 0.46220E+06
| 0.40012E+06
| 0.48602E+06
| 42
| 0.11930E+07
| 0.14567E+07
| 0.12808E+07
| 43
| 0.11116E+07
| 0.86010E+06
| 0.10009E+07
| 81
| 0.51636E+06
| 0.98414E+06
| 0.97578E+06
| 82
| 0.19435E+06
| 0.11272E+07
| 0.15469E+07
| 83
| 0.74558E+06
| 0.54880E+06
| 0.47220E+06
| 84
| 0.46220E+06
| 0.40012E+06
| 0.48602E+06
| 85
| 0.11930E+07
| 0.14567E+07
| 0.12808E+07
| 86
| 0.11116E+07
| 0.86010E+06
| 0.10009E+07
|
1.优化前受力分析
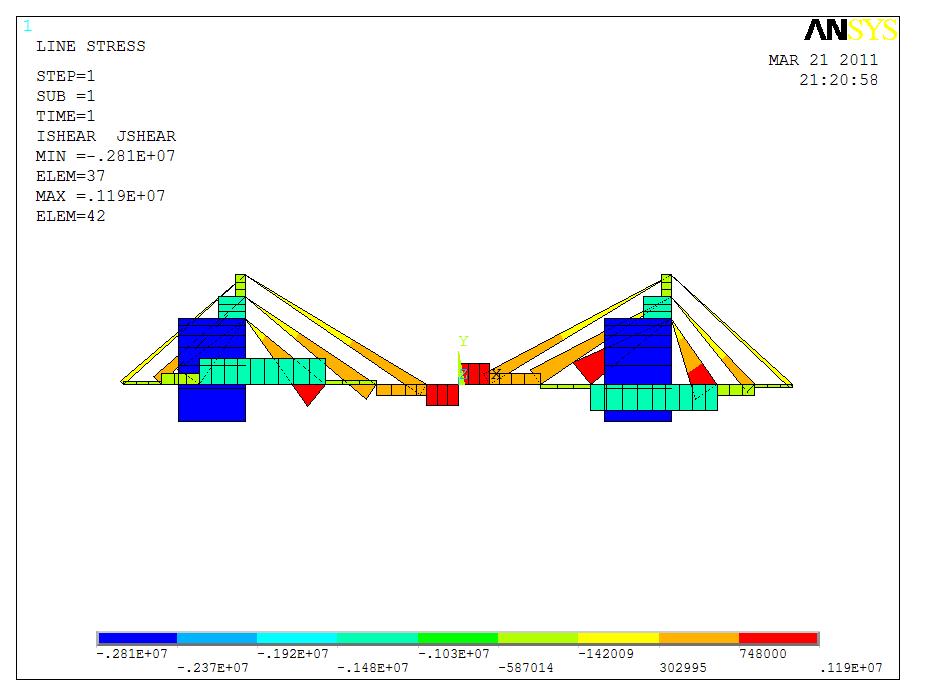 轴力图
轴力图
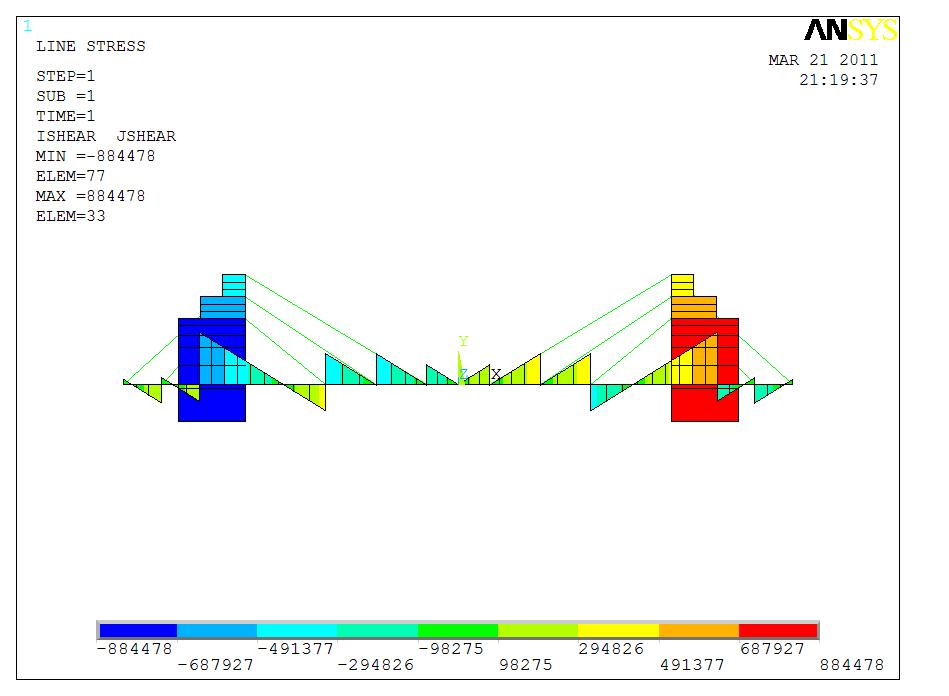 剪力图
剪力图
弯矩图 竖向变形图
2.只考虑主梁应变能最小
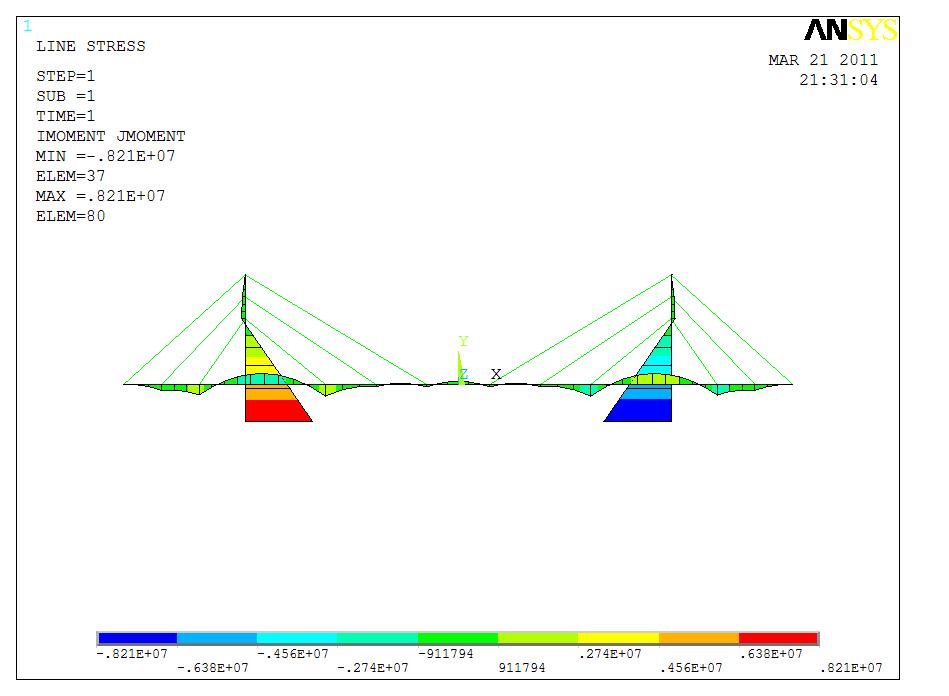 弯矩图
弯矩图
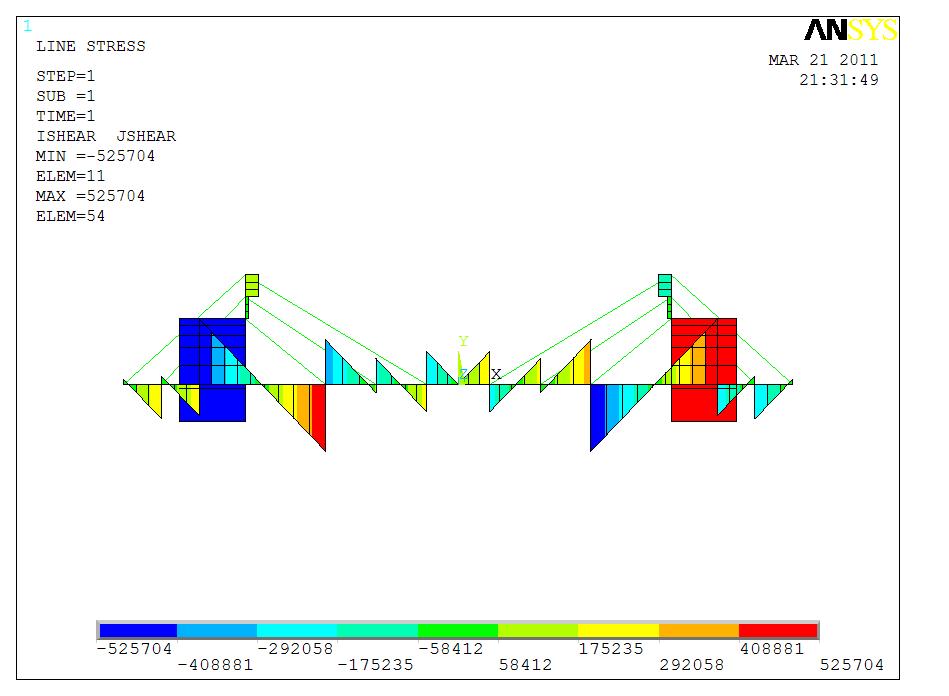 剪力图
剪力图
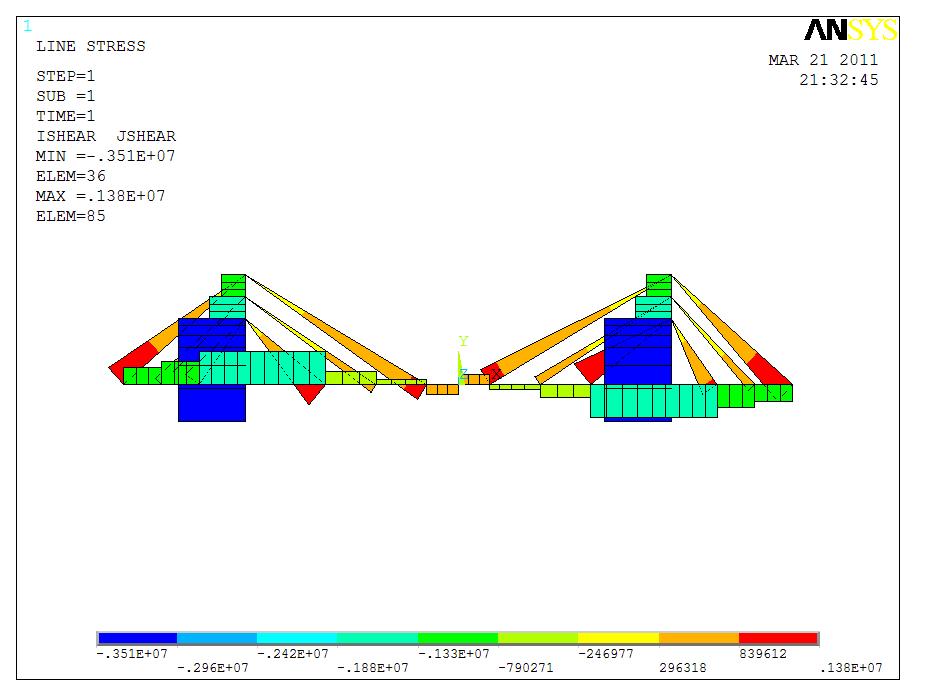 轴力图
轴力图
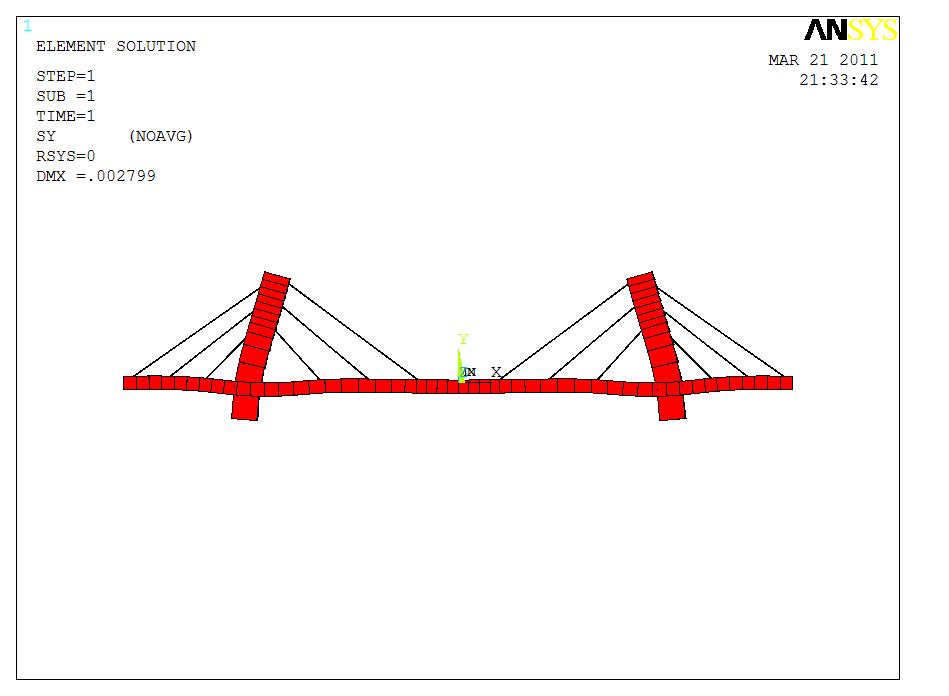 竖向变形图
竖向变形图
3.主梁和塔的应变能最小 弯矩图 剪力图 轴力图 竖向变形图
|